找环，奇的！（1s/512MB）

题目描述

给定一个 $n$ 个点， $m$ 条边的无向图，编号从 $1$ 到 $m$ 。

有 $q$ 个询问，每次给出一个区间 $[l_i,r_i]$ 表示编号在区间内的边无法使用，你要判断能不能在剩下的边中找到奇环。

形式化的说，一个奇环为一个形如 $S,s_1,s_2,\ldots,s_k,S$ 的序列（要求 $k$ 为偶数），其中 $S$ 和 $s_1$，$s_k$ 和 $S$，以及 $\forall 1 \lt i \leq k$，$s_{i-1}$ 和 $s_i$ 之间都有可用的边直接相连。

输入格式

输入第一行三个整数 $n,m,q$。

接下来 $m$ 行，第 $i$ 行两个整数 $u,v$（保证 $u \neq v$），描述了编号为 $i$ 的边。保证无重边。

接下来 $q$ 行，第 $i$ 行两个整数 $l_i,r_i$，表示询问。

输出格式

输出 $q$ 行。

在第 $i$ 行，若第 $i$ 天可以找到奇环，输出 YES，否则输出 NO。

样例一

输入

6 8 2
1 3
1 5
1 6
2 5
2 6
3 4
3 5
5 6
4 8
4 7

输出

NO
YES

样例解释

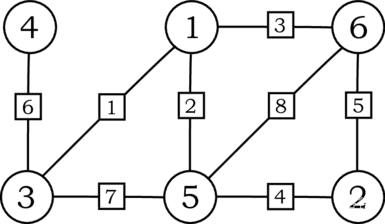
子任务

所有数据均满足：$1 \leq n,m,q \leq 2 \times 10^5$。

• 子任务 1（6 分）：$1 \leq n,m,q \leq 200$；
• 子任务 2（8 分）：$1 \leq n,m,q \leq 2 \times 10^3$；
• 子任务 3（25 分）：$\forall i \in [1,q]$，$l_i =1$；
• 子任务 4（10 分）：$\forall i \in [1,q]$，$l_i \leq 200$；
• 子任务 5（22 分）：$q \leq 2 \times 10^3$；
• 子任务 6（29 分）：无特殊限制。